「ゼロから作るDeepLearning」を写経してみる(4)「4章ニューラルネットワークの学習」
Deep Learningを学んでみたいので、以下の本を写経している。
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装 単行本(ソフトカバー) – 2016/9/24
斎藤 康毅 (著)
3672円
サポートサイト
https://github.com/oreilly-japan/deep-learning-from-scratch
前回は、3章を写経した。ニューラルネットワークの初歩を、pythonで実装してみたんは楽しかった。
今回は、4章 ニューラルネットワークの学習 を写経してみる。
(環境)
Windows8.1
Python 3.5.2
Anaconda 4.1.1 (64-bit)
Jupyter Notebook (ipython) 4.2.0
(0)Git Bash here(cmd.exe コマンドプロンプトもOK) で、jupyter notebook
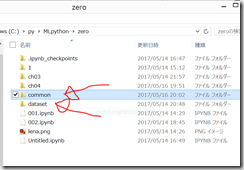
ファイル構成はこんな感じ
ここに、ch04 というフォルダを作成し、その中でスクリプトを書いていく。
(上記サポートサイトからダウンロードしたファイル群を、dataset の中に保存し、そちらから利用するため。)
(1)データから学習する
5 → 人の考えたアルゴリズム → 答え
5 → 人の考えた特徴量(SIFT, HOGなど) → 機械学習(SVN, KNNなど) → 答え
5 → ニューラルネットワーク(Deep Learning) → 答え
訓練データとテストデータ
(2)損失関数 loss function : ニューラルネットワークの学習で用いられる指標
一般には、「2乗和誤差」や「交差エントロピー誤差」などが用いられる。
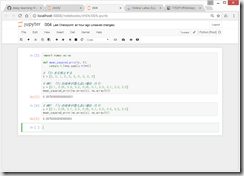
●2乗和誤差 mean squared error

E = \frac{1}{2} \sum_k ( y_{k} - t_{k})^{2}
yk : ニューラルネットワークの出力
tk : 教師データ
k : データの次元数
たとえば、第3章の手書き数字認識の例では、
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
one-hot 表現 : 正解ラベルを1として、それ以外は0で表す表記法
●交差エントロピー誤差

E = - \sum_k t_{k} \log y_{k}
yk : ニューラルネットワークの出力
tk : 正解ラベル (正解ラベルとなるインデックスだけが1で、その他は0(one-hot表現))
●ミニバッチ学習
例えば、60,000枚の訓練データの中から100枚を無作為に選び出して、その100枚を使って学習を行う方法を、ミニバッチ学習という。
●なぜ損失関数を設定するのか?
→認識精度を指標にすると、パラメータの微分がほとんどの場所で0になってしまうため、学習が困難になってしまうため、微分可能である損失関数を設定して、指標とする。
(3)微分
なつかしい微分の定義

\frac{df(x)}{dx} = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}
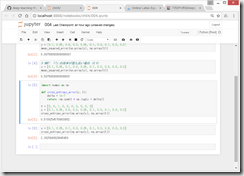
数値微分 numerical differentiation
丸め誤差 rounding error
●偏微分

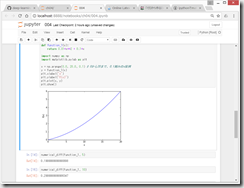
f( x_{0}, x_{1} ) = x_{0}^{2} + x_{1}^{2}
数値微分 numerical differentiation
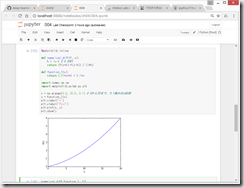
●勾配
すべての変数の偏微分をベクトルとしてまとめたものを勾配gradientという。
→ 勾配が示す方向は、各場所において関数の値を最も減らす方向である。
https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/ch04/gradient_2d.py
(4)勾配法 gradient method
機械学習の問題の多くは、学習の際に最適なパラメータを探索する。
ニューラルネットワークも、最適な(=損失関数が最小値をとるとき)パラメータ(重みとバイアス)を学習時に見つける必要がある。
しかし、損失関数は複雑なので、勾配をうまく利用して関数の最小値を探そうとするのが勾配法。
→個人的なイメージ的としては、極小値ばっかり探してしまう危険性をはらんでいると思うが、まあ、そういうものなのでしょう。

x_{0} = x_{0} - \eta \frac{\partial f}{\partial x_{0} } \\
x_{1} = x_{1} - \eta \frac{\partial f}{\partial x_{1} }
η(イータ)は、更新の量を表し、ニューラルネットワークの学習においては、学習率 learning rateと呼ばれる。
学習率η(イータ)は、大きすぎても小さすぎても、「良い場所」にたどり着くことができないので、学習率の値を変更しながら、正しく学習できているかどうか、確認作業を行うのが一般的とのこと。
ちなみに、偏微分の∂は「パーシャル、ラウンド・ディー」と読むらしい。
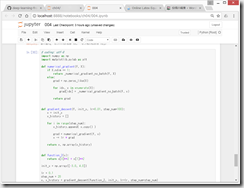
https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/ch04/gradient_method.py
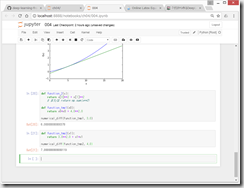
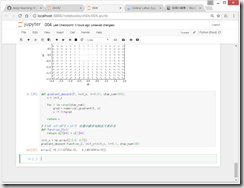
学習率が大きすぎる例:lr=10.0
→下の例では、なんかすごく大きな値になってしまっている。
学習率が小さすぎる例:lr=1e-10
→下の例では、100回程度では、全然動かない。100回動いても、まだスタート地点にいる感じ。
●ニューラルネットワークに対する勾配
形状が2x3の重みWだけを持つニューラルネットワーク。

W = \left(
\begin{array}{ccc}
w_{11} & w_{21} & w_{31} \\
w_{12} & w_{22} & w_{32}
\end{array}
\right)
損失関数をLで表す場合、勾配は、以下のようになる。

\frac{\partial L}{\partial W} = \left(
\begin{array}{ccc}
\frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{31}} \\
\frac{\partial L}{\partial w_{12}} & \frac{\partial L}{\partial w_{22}} & \frac{\partial L}{\partial w_{32}}
\end{array}
\right)
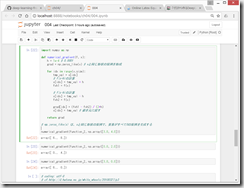
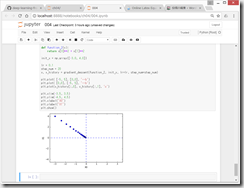
ニューラルネットワークにおいて、勾配を求める実装
https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/ch04/gradient_simplenet.py
そろそろしんどくなっていたので、
https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/ch04/gradient_simplenet.py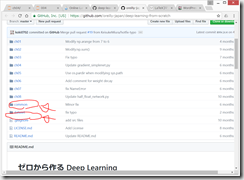
から、common/ フォルダと、dataset/ フォルダを、中身ごとダウンロードしておく。
(softmax, cross_entropy_srror 関数などを、取り込むため。)
ニューラルネットワークの勾配を求めれば、後は、勾配法に従って、重みパラメータを更新することになる。
(5)学習アルゴリズムの実装
確率的勾配降下法(stochastic gradient descent, SGD)
step1 ミニバッチ
step2 勾配の算出
step3 パラメータの更新
step4 繰り返す
ここでは、2層のニューラルネットワーク(隠れ層が1層のネットワーク)を対象に、MNISTデータセットを使って学習を行う。
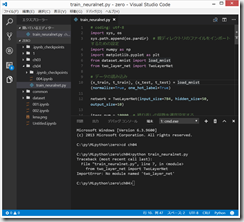
TwoLayerNet
https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/ch04/two_layer_net.py
何故かわからないが、ここはうまくいかず。。。
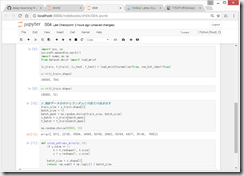
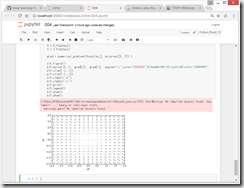
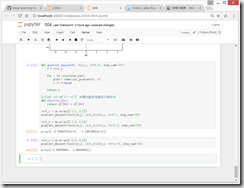
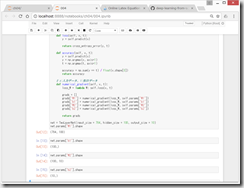
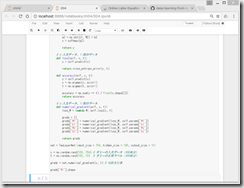
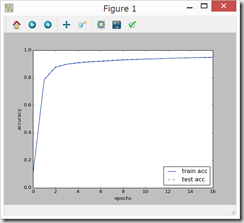
●ミニバッチ学習の実装
ミニバッチ学習とは、訓練データから無作為に一部のデータを取り出して(=ミニバッチ)、そのミニバッチを対象に、勾配法によりパラメータを更新する学習。
two_layer_net をimportする必要があるとのこと。
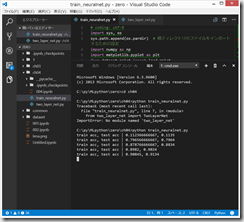
2回、
python train_neuralnet.py
すると、微妙に異なる結果になるところが面白い。
最後の方は、jupyter notebookで、なぜかうまくできなかったので、あきらめて、サポートサイトのソースコードをコピペしてしまった。。。
でも、なんとなく、雰囲気はつかめた気がしたので、よしとする。
次は、いよいよ、1回目に読んだときは全く理解できなかった、「5章 誤差逆伝播法」に突入予定である。
(参考)Online Latex Equation Editor – Sciweavers
http://www.sciweavers.org/free-online-latex-equation-editor




ディスカッション
コメント一覧
まだ、コメントがありません