「詳解ディープラーニング」を写経してみる(3)3.5多クラスロジスティック回帰
前回は、3.4 ロジスティック回帰 を写経してみた。
http://twosquirrel.mints.ne.jp/?p=19070
詳解 ディープラーニング TensorFlow・Kerasによる時系列データ処理 Kindle版
巣籠 悠輔 (著)
3400円
出版社: マイナビ出版 (2017/5/30)
ソースコード
https://github.com/yusugomori/deeplearning-tensorflow-keras
今回は、3.5 多クラスロジスティック回帰 を写経してみたい。背景のところの数式がさっぱりわからなくて悲しい。
(環境)
Windows8.1
Python 3.5.2
Anaconda 4.1.1 (64-bit)
Tensorflow 1.2.1
Keras 2.0.6
(0)多クラスロジスティック回帰について
2010-04-30
ロジスティック回帰
http://aidiary.hatenablog.com/entry/20100430/1272590402
13分でわかるロジスティック回帰
Takatymo
2016年01月08日に更新
http://qiita.com/Takatymo/items/fb16c088de325d98a363
2016-11-30
出力層で使うソフトマックス関数
http://s0sem0y.hatenablog.com/entry/2016/11/30/012350
2017-06-11
softmax関数の学習まとめ 〜特徴と確率との関係〜
http://www.python-deeplearning.com/entry/2017/06/11/115131
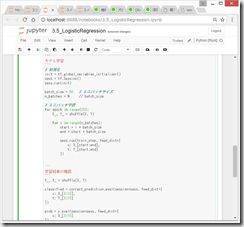
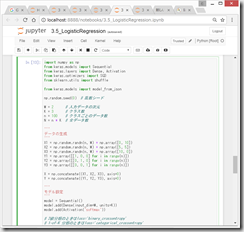
(1)Tensorflowでの実装
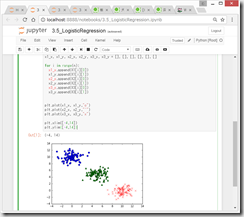
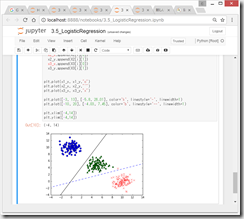
プロット
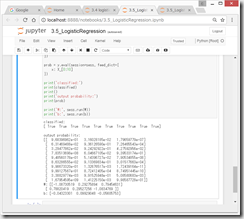
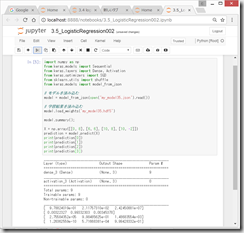
(2)Wとbを求める。
Wとbを求める。
print('W:’, sess.run(W))
print('b:’, ses.run(b))
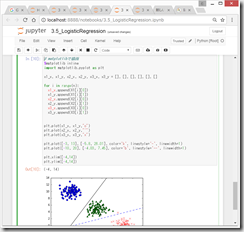
(3)境界線の図示
クラス1とクラス2の境界の直線は、
w11x1+w12x2+b1 = w21x1+w22x2+b2
<=> -1.09x+0.8y-0.04=0.30x+0.10y+0.10 (おおざっぱに計算)
<=> -1.39x+0.7y-0.14=0
となるとのこと。
(-3, -5.8)と、(13, 26.01)を通る直線
plt.plot([-3, 13], [-5.8, 26.01], color=’k’, linestyle=’-', linewidth=1)
同様に、クラス2とクラス3の境界の直線は、
w21x1+w22x2+b2 = w31x1+w32x2+b3
<=> 0.30x+0.10y+0.10 =0.79x-1.08y-0.06 (おおざっぱに計算)
<=> 0 = 0.49x-1.28y-0.26
となるとのこと。
(-10, -4.03)と、(20, 7.45)を通る直線
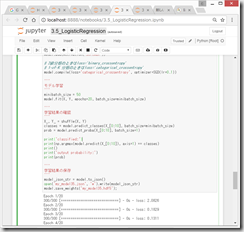
(4)kerasでの多クラスロジスティック回帰の実装
の後に、
from keras.models import model_from_json
"’
学習結果の保存
"’
model_json_str = model.to_json()
open('my_model35.json’, 'w’).write(model_json_str)
model.save_weights('my_model35.hdf5’);
を加えて実行。
同じフォルダ内に、以下の2つのファイルが作成される。
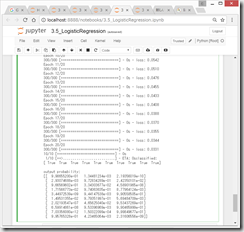
(5)外部ファイルからモデルと学習結果を取り込んで予測。
なぜか、最初はうまくいかなかったが、jupyter notebookを一旦終了してから再開して、さらにごちゃごちゃやっていたら、いつの間にか、読み込んで計算してくれた。
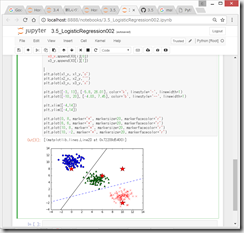
たしかに、図示すると、それぞれ、クラス1、クラス2、クラス2、クラス3に分類されており、いい感じ。
上記グラフのソースコード
https://gist.github.com/adash333/5212109e85228c9f4e38527c539a7462
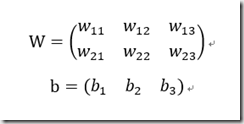



ディスカッション
コメント一覧
まだ、コメントがありません