Rでt検定

１．どのような場合にt検定を用いることができるのか？

2群が独立しており、

（１）各群のデータが正規分布に従う　⇒ 両群の分散が等しければ、t検定。分散が等しくなければ、Welch検定を用いる。

（２）各群のデータが正規分布に従わない、あるいは順序変数 ⇒ Mann-Whitney U検定

２．各群が正規分布に従うかどうかの判定”Kolmogorov-Smirnov検定（ks.test()関数）”

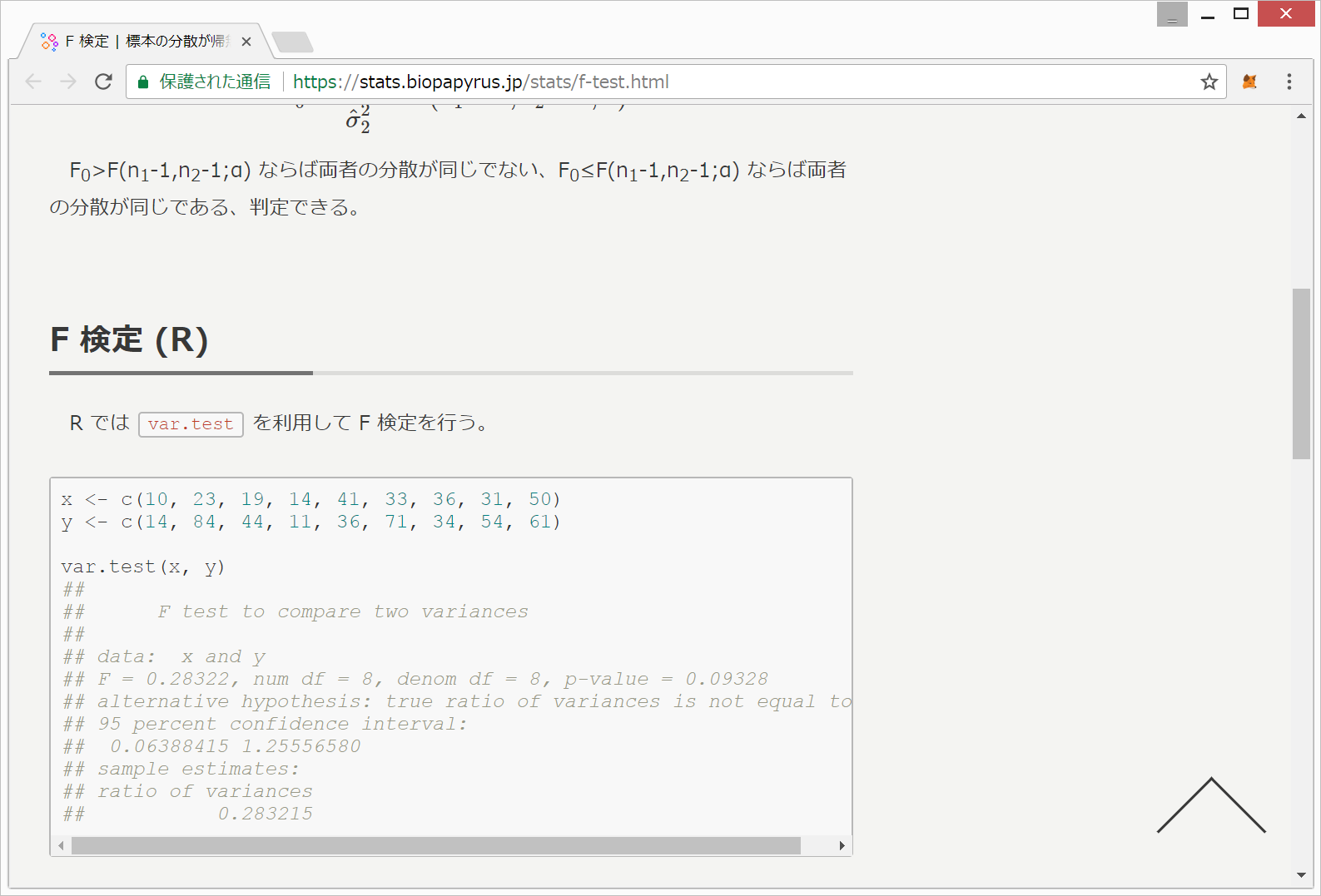
３．正規分布に従う2群の分散が等しいかどうかの判定”F検定（var.test()関数）”

F検定の後にt検定することについては、議論があるらしいが、気にしないことにする。

標本の分散が帰無仮説に従うかどうかを検定

F 検定

2018.01.12

https://stats.biopapyrus.jp/stats/f-test.html

p>0.05であれば、2群は分散が等しいと言えるので、2群の平均値を比較するときはt検定を用いる。

p>0.05であれば、2群は分散が等しいとは言えないので、2群の平均値を比較するときはWelch検定を用いることになる。

４．t検定"t.test(group1, group2, paired=F)"

p<0.05であれば、2群の平均値に有意差あり。

p>0.05であれば、2群の平均値に有意差無し。

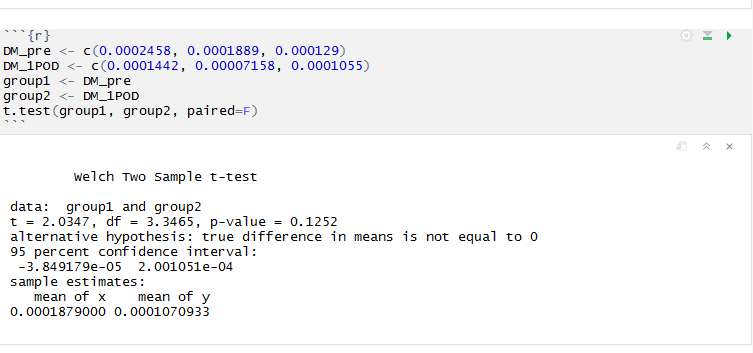
DM_pre <- c(0.0002458, 0.0001889, 0.000129)
DM_1POD <- c(0.0001442, 0.00007158, 0.0001055)
group1 <- DM_pre
group2 <- DM_1POD
t.test(group1, group2, paired=F)

R Studioでの実行結果（F検定は行っていない）

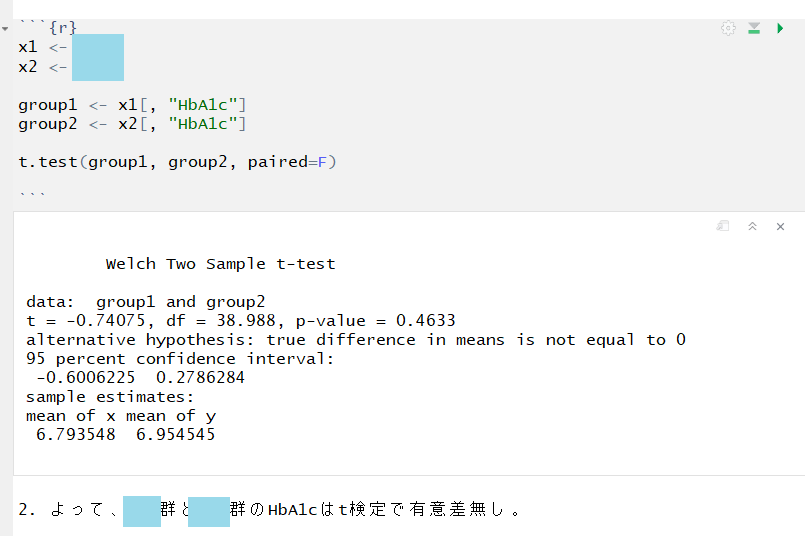
元データが表になっている場合

x1 <- data1
x2 <- data2
 
group1 <- x1[, "HbA1c"]
group2 <- x2[, "HbA1c"]
 
t.test(group1, group2, paired=F)

５．Welch検定"t.test(group1, group2, var.equal=F, paired=F)"

t.test()関数の中で、var.equal=F と入れればWelch検定ができる。

p<0.05であれば、2群の平均値に有意差あり。

p>0.05であれば、2群の平均値に有意差無し。

６．Mann-Whitney U検定

http://cse.naro.affrc.go.jp/takezawa/r-tips/r/65.html

上記サイトでは、ウィルコクソンの順位和検定と、マン・ホイットニーの U 検定が同じであると記載されている.

Wilcoxon-Mann-Whitney検定（WMW検定）

https://oku.edu.mie-u.ac.jp/~okumura/stat/wmw.html

Rによるウィルコクソンの順位和検定

http://data-science.gr.jp/implementation/ist_r_wilcoxon_rank_sum_test.html

ウィルコクソンの順位和検定は2群間に対応がない場合に使う．この検定法はパラメトリック検定でいうところのスチューデントのt検定とかウェルチのt検定に相当する．

上記サイトよりコードを引用。

install.packages("exactRankTests", repos="http://cran.ism.ac.jp/")
library(exactRankTests)

wilcox.exact(x=vx,y=vy,paired=F)

memo

ks.test()関数を用いるときは、下記コードでは、y1[“sBP_00pre”]ではエラーになる。正しくは、y1$sBP_00preのように記載する。データフレームとリストの違い？

y1 <- subset(x2, Hb_Improve=="TRUE")
y1 <- y1$sBP_00pre
ks.test(x=y1,y="pnorm",mean=mean(y1),sd=sd(y1))

参考リンク

Rによるウェルチのt検定

http://data-science.gr.jp/implementation/ist_r_welch_t_test.html

参考文献

EZRで行う場合は、下の本のp92以降が非常に分かりやすいです。

サルでもわかる機械学習